Quicksort

Nama: Haryo Fajar Bhagaskoro
NPM : 54414833
DOSEN : Kunto Bayu A, ST
MATKUL : Algoritma & Pemrograman 1A


Quicksort merupakan Algoritma Sorting yang dikembangkan oleh Tony Hoare yang, secara kasus rata-rata, membuat pengurutan O(n log n) untuk mengurutkan n item. Algoritma ini juga dikenal sebagai Partition-Exchange Sort atau disebut sebagai Sorting Pergantian Pembagi. Pada kasus terbentuknya, algoritma ini membuat perbandingan O(n²), malaupun kejadian seperti ini sangat langka. Quicksort sering lebih cepat dalam praktiknya dari pada algoritma O(n log n) yang lainnya. Dan juga, urutan dan referensi lokalisasi memori quicksort bekerja lebih baik dengan menggunakan cache CPU, jadi keseluruhan sorting dapat dilakukan hanya dengan ruang tambahan O(log n).
Quicksort merupakan sorting pembanding dan pada implementasi efisien tidak merupakan algoritma sorting yang stabil.
contoh quicksort


ALGORITMA
Quicksort merupakan Algoritma Pembagi. Pertama sekali quicksort membagi list yang besar menjadi dua buah sub list yang lebih kecil: element kecil dan element besar. Quicksort kemudian dapat menyortir sub list itu secara rekursif.
Langkah-Langkah pengerjaannya ialah:

1. Ambil sebuah elemen, yang disebut dengan pivot, pada sebuah daftar.
2. Urutkan kembali sebuah list sehingga elemen dengan nilai yang kecil dari pivot berada sebelum pivot, sedangkan seluruh element yang memiliki nilai yang lebih besar dari pivot berada setelahnya (nilai yang sama dapat berada pada pivot setelahnya). Setelah pemisahan, pivot berada pada posisi akhirnya. Operasi ini disebut Partition.
3. Sub list kemudian disortir secara recursif dari elemen yang lebih kecil dan sub list dari elemen yang lebih besar.

Kasus dasar dari rekusrif ialah list dari besaran nol atau satu, yang tidak perlu untuk di sorting.

Versi Sederhana
Dalam Pseudocode sederhana, Algoritmanya dapat dinyatakan sebagai berikut:

  function quicksort('array')
      if length('array') ≤ 1
          return 'array'  // an array of zero or one elements is already sorted
      select and remove a pivot value 'pivot' from 'array'
      create empty lists 'less' and 'greater'
      for each 'x' in 'array'
          if 'x' ≤ 'pivot' then append 'x' to 'less'
          else append 'x' to 'greater'
      return concatenate(quicksort('less'), 'pivot', quicksort('greater')) // two recursive calls

Contoh keseluruhan dari quicksort pada kumpulan acak dari angka. Element yang gelap merupakan pivot. Pivot selalu dipilih sebagai element terakhir pada partisi. Bagaimanapun, selalu memilih elemen terakhir pada partisi sebagai pivot sehingga hasil pada kasus terburuk () pada daftar yang telah diurutkan, atau daftar yang serupa. Karena elemen yang sama memotong hingga pada akhir dari prosedur soring pada jumlah yang besar, versi dari algoritma quicksort yang memilih pivot sebagai elemen tengah berjalan lebih cepat dari pada algortima yang dijelaskan pada diagram ini pada sejumlah besar angka.

Perlu diperhatikan bahwa kita hanya memeriksa elemen dengan membandingkan mereka pada elemen yang lain. Prosedur ini disebuk Sorting Pembandingan. Jenis ini juga merupakan jenis sorting yang stabil (asumsikan bahwa untuk setiap method menerima elemen pada urutan aslinya dan pivot yang dipilih merupakan elemen terakhir dari nilai yang sama).
Kebenaran dari algoritma partisi didasari pada dua argumen berikut:

• Pada setiap iterasi, seluruh elemen diproses selama ini berada pada posisi yang diinginkan: sebelum pivot lebih kurang dari nilai pivot, setelah pivot lebih besar dari nilai pivot (Invarian Loop).

Kebenaran dari keseluruhan algortima dapat dibuktikan dengan penyederhanaan fakta: untuk elemen nol atau satu, algoritma tidak akan mengubah data; untuk jumlah data yang lebih besar, algoritma akan menghasilkan dua bagian, elemen yang kurang dari pivot dan elemen yang lebih besar dari nya, data ini sendiri akan diurutkan secara hipotesa rekursif.

Contoh dari penerapan Quicksort.

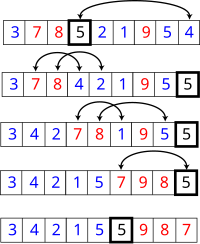
Partisi ditepat bekerja pada daftar yang kecil. Elemen kotak merupakan element pivot, elemen berwarna biru merupakan elemen yang bernilai kecil atau sama, dan elemen yang berwarna merah lebih besar.

 Versi In-Place

Kerugian dari versi sederhana diatas membutuhkan ruang simpan O(n) yang lebih besar, yang sama buruknya seperti merge sort. Memory tambahan yang dibutuhkan dapat juga secara radikal berpengaruh pada kecepatan dan performa cache pada implementasi praktiknya. Terdapat juga versi yang lebih rumit yang menggunakan algoritma partisi in-place dan dapat mencapai urutan lengkap menggunakan ruang O(logn) (tidak dihitung input) pada rata-rata (untuk sekali pemanggilan tumpukan). Kita mulai dengan fungsi partisi:

   // left is the index of the leftmost element of the array
   // right is the index of the rightmost element of the array (inclusive)
   //   number of elements in subarray = right-left+1
   function partition(array, 'left', 'right', 'pivotIndex')
      'pivotValue' := array['pivotIndex']
      swap array['pivotIndex'] and array['right']  // Move pivot to end
      'storeIndex' := 'left'
      for 'i' from 'left' to 'right' - 1  // left ≤ i < right
          if array['i'] < 'pivotValue'
              swap array['i'] and array['storeIndex']
              'storeIndex' := 'storeIndex' + 1
      swap array['storeIndex'] and array['right']  // Move pivot to its final place
      return 'storeIndex'

Ini merupakan Algoritma Partisi In-Place. algortima ini memisahkan bagian dari array antara index kiri dan kanan secara inklusif, dengan memindahkan seluruh elemen kurang dari array[pivotIndex] sebelum pivot, dan elemen yang sama atau lebih besar darinya. Dalam prosesnya, algoritma ini juga mencari posisi akhir untuk elemen pivot, yang kembali. algoritma ini secara sementara memindahkan elemen pivot pada akhir dari subarray, sehingga tidak mengganggu proses algoritma. Karena hanya menggunakan penukaran, list akhir memiliki elemen yang sama seperti elemen awalnya. Perlu diperhatikan bahwa elemen ditukan beberapa kali sebelum mencapai tempat akhirnya. Dan juga, jika pivot itu ganda pada inputan array, mereka dapat menyebar pada subarray kanan, pada urutan apapun. Cara ini tidak mewakili kesalahan dalam membagi, dimana pengurutan lebih lanjut akan memindahkan dan akhirnya merekatkan mereka bersama.
Setelah kita memiliki ini, menulis quicksort sendiri ialah mudah:

function quicksort(array, 'left', 'right') // If the list has 2 or more items if 'left' < 'right' // See "Choice of pivot" section below for possible choices choose any 'pivotIndex' such that 'left' ≤ 'pivotIndex' ≤ 'right' // Get lists of bigger and smaller items and final position of pivot 'pivotNewIndex' := partition(array, 'left', 'right', 'pivotIndex') // Recursively sort elements smaller than the pivot quicksort(array, 'left', 'pivotNewIndex' - 1) // Recursively sort elements at least as big as the pivot quicksort(array, 'pivotNewIndex' + 1, 'right')

Setiap pemanggilan rekursif pada fungsi quicksort ini mengurangi besar dari array yang akan diurutkan paling tidak satu elemen, semenjak setiap elemen pada pivotNewIndex diletakkan pada posisi akhirnya. Oleh karena itu, algoritma ini menjamin mengakhiri pemanggilan rekursif pada paling banyak n pemanggilan. Bagaimanapun, versi dari quicksort ini tidak stabil semenjak pengurutan elemen partisi hanya dilakukan pada satu partisi.

Daftar Pustaka http://id.wikipedia.org/wiki/Quicksort